[Econometrics] Regression Analysis with Time Series Data and Assumptions
An obvious characteristic of time series data that distinguishes them from cross-sectional data is temporal ordering. In time series analysis, the past can affect the future, but not vice versa. Another difference between cross-sectional and time series data is randomness. In cross-sectional analysis, random outcomes are fairly straightforward. Randomness is justified by random sampling. However, randomness in time series data is justified naturally because the outcomes of time series variables are not foreknown.
Static Models
Suppose that we have time series data available on two variables, say y and z, where yt and zt are dated contemporaneously.

Static regression models are also used when we are interested in knowing the tradeoff between y and z.
Finite Distributed Lag (FDL) Models
In a finite distributed lag (FDL) model, we allow one or more variables to affect y with a lag.
One example of FDL model is shown as

z is a constant, equal to c, in all time periods before time t. At time t, z increases by one unit to c + 1 and then reverts to its previous level at time t + 1.

To focus on the ceteris paribus effect of z on y,

From the two equations, yt - y(t-1) = δ0, which means that δ0 is the immediate change in y due to the one unit increase in z at time t. δ0 is usually called the impact propensity or impact multiplier. At the time t + 3, y has reverted to its initial level: y(t+3) = y(t-1).
------------------------------------------------------------------------------
We are also interested in the change in y due to a permanent increase in z. Before time t, z equals the constant c. At time t, z increases permanently to c + 1: zs = c, s < t and zs = c + 1, s >= t, setting the errors to zero.
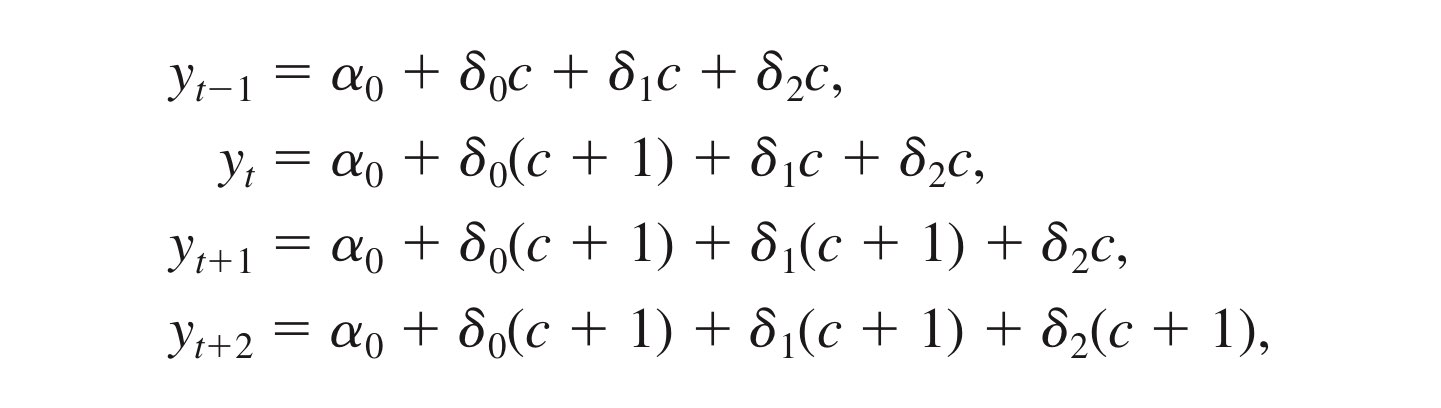
With the permanent increase in z, after one period, y has increased by δ0 + δ1, and after two periods, y has increased by δ0 + δ1 + δ2. This shows that the sum of the coefficients on current and lagged z, δ0 + δ1 + δ2 is the long run change in y given a permanent increase in z and is called the long-run propensity(LRP) or long-run multiplier. For any horizon h, we can define the cumulative effect as δ0 + δ1 + δ2.....δh, which is interpreted as the change in the expected outcome h periods after a permanent, one-unit increase in x.
LRP = δ0 + δ1 + δ2.....δh
Finite Sample Properties of OLS under Classical Assumptions
Assumption TS.1 Linear in Parameters
The stochastic process {(xt1, xt2.....,xtk, yt): t = 1, 2...., n} follows the linear model
yt = β0 + β1xt1 + β2xt2 ..... + βkxtk + ut,
where {ut : t = 1, 2, ...., n} is the sequence of errors or disturbances. Here, n is the number of observations(time periods). xt1 = z1, xt2 = z2, ....
Assumption TS.2 No Perfect Collinearity
In the sample (and therefore in the underlying time series process), no independent variable is constant nor a perfect linear combination of the others.
Assumption TS.3 Zero Conditional Mean
For each t, the expected value of the error ut, given the explanatory variables for all time periods, is zero.
E(ut| xt1, xt2.... xtk) = E(ut|xt) = E(ut|X) = 0, t = 1, 2,.... , n
Assumption TS.3 implies that the error at time t, ut is uncorrelated with each explanatory variable in every time period. The fact that this is stated in terms of the conditional expectation means that we must also correctly specify the functional relationship between yt and the explanatory variables. If ut is independent of X and E(ut) = 0, then Assumption TS.3 automatically holds. (시간에 관계없이 항상) When this assumption holds, we say that xtj are contemporaneously exogenous and uncorrelated: Corr(utk, ut) = 0, for all j.
In a time series context, random sampling is almost never appropriate, so we must explicitly assume that the expected value of ut, is not related to the explanatory variables in any time period. (cross-sectional의 경우는 random sampling을 통해서 독립변수들과 ui 자동적으로 독립임을 증명해주었는데, 시계열 변수들은 직접 증명해주어야 함)
+ Anything that causes the unobservables at time t to be correlated with any of the explanatory variables in any time period causes Assumption TS.3 to fail. And in the social sciences, many explanatory variables may very well violate the strict exogeneity assumption. ex) the amount of labor input might not be strictly exogenous, as it is chosen by the farmer, and the farmer may adjust the amount of labor based on last year's yield.
Even though Assumption TS.3 can be unrealistic, we begin with it in order to conclude that the OLS estimators are unbiased. Assumption TS.3 has the advantage of being more realistic about the random nature of the xtj, while it isolates the necessary assumption about how ut, and explanatory variables are related in order for OLS to be unbiased.
Unbiasedness of OLS
Under assumptions TS.1 -3, the OLS estimators are unbiased conditional on X, and therefore unconditionally as well:
E(^βj) = βj, j = 0, 1, ....., k.
Assumption TS.4 Homoskedasticity
Conditional on X, the variance of ut, is the same for all t : Var(ut|X) = Var(ut) = σ^2
This assumption requires that the unobservables affecting interest rates have constant variance over time.
경제지표 관련 회귀 선 내 ut에 interest rate가 t에 따라 변동하면 heteroskedasticity. 즉, constant해야 homoskedasticity.
Assumption TS.5 No serial Correlation
Conditional on X, the errors in two different time periods are uncorrelated: Corr(ut, us| X) = 0, for all t
≠ s. (Simply, Corr(ut, us) = 0m for all t ≠ s)
When this assumption is false, we say that the errors in this assumption suffer from serial correlation or, autocorrelation, because they are correlated across time. Consider the case of errors from adjacent time periods. Suppose that when u(t-1) > 0 then, on average, the error in the next time period, ut, is also positive. Then, Corr(ut, u(t-1)) > 0, and the errors suffer from serial correlation. In other words, TS.5 assumes nothing about temporal correlation in the independent variables.
Under Assumptions TS.1 through TS.5, the OLS estimators are the best linear unbiased estimators conditional on X.
Assumption TS.6 Normality
The errors ut, are independent of X and are independently and identically distributed as Normal(0,σ^2)
Resource : Jeffrey M. Woolderfige, "Introductory Econometrics : A Modern Approach 5th edition"